プレゼンテーションの社会物理学：グラノヴェッターの閾値モデルと社会的相転移のエンジニアリング

2025.11.28

序論：説得の科学から場の物理学へ

プレゼンテーションの本質とは何か。伝統的なレトリックの観点からは、それは話者の「ロゴス（論理）」「パトス（情熱）」「エトス（信頼）」によって聴衆個々人を説得するプロセスとして理解されてきた。しかし、数百人、あるいは数千人の聴衆を前にした時、そこで発生する現象は単なる一対一のコミュニケーションの総和ではない。それは、物理学における相転移――水が氷になる、あるいは磁石が磁性を帯びるような、システム全体の状態変化――に極めて類似した挙動を示す。静まり返った会場が、ある瞬間を境に熱狂的なスタンディングオベーションへと変化する。あるいは、誰もが心の中では同意しているにもかかわらず、誰一人として手を挙げない「凍りついた」状態が続く。これらの現象は、個人の心理学だけでは説明がつかない。

社会学者マーク・グラノヴェッターが1978年に提唱した「閾値モデル（Threshold Models of Collective Behavior）」は、この集団ダイナミクスの謎を解くための強力なレンズを提供する ¹。このモデルは、個人の意思決定が集団全体の動向にどのように依存するかを数理的に記述し、微細な個人の行動変化がいかにしてマクロな社会現象（暴動、普及、喝采）を引き起こすかを明らかにした。

本報告書では、グラノヴェッターの理論を基盤としつつ、統計力学におけるイジングモデル、ネットワーク科学における紐帯の理論、そして最新の社会物理学における「25%のティッピング・ポイント」の知見を統合し、プレゼンテーションという「場」をエンジニアリングするための包括的な科学的フレームワークを提示する。聴衆を説得するのではなく、聴衆という系（システム）のパラメータを操作し、狙った状態へと相転移させるための物理学を詳述する。

第1章集団行動の数理モデル：グラノヴェッターの革命

1.1 合理的選択と集団のパラドックス

集団行動の研究において長らく支配的だったのは、集団心理や群衆心理といった、個人の理性が集団の中で埋没するという見方であった。しかし、グラノヴェッターのアプローチは根本的に異なる。彼は、個人は集団の中にいても依然として合理的であり、コストとベネフィットを計算して行動していると仮定した。ただし、その計算式の中に「他者の行動数」という変数が組み込まれている点が革新的であった ¹。

従来の社会調査では、個人の選好（好みや意見）の平均値を知れば、集団の行動が予測できると考えられてきた。例えば、聴衆の80%が講演内容に好意的であれば、会場は大いに盛り上がるはずだと予測する。しかし、現実にはそうならないことが多い。好意的な聴衆が沈黙したまま終わることもあれば、少数の扇動者が群衆全体を暴徒化させることもある。

グラノヴェッターはこのパラドックスに対し、「集団の結果（マクロ）は、個人の選好（ミクロ）の単なる総和や平均ではない」と断じた ⁴。集団の振る舞いを決定するのは、個人の平均的な意欲ではなく、意欲の「分布」、特にその分布の「連続性」である。これは、金属の強度が平均的な原子結合力ではなく、結晶構造の欠陥（転位）によって決まるのと同様に、社会構造の微細な欠陥が全体の帰結を左右することを示唆している。

1.2 閾値（Threshold）の定義と効用関数

このモデルの中核をなす概念が「閾値（Threshold）」である。閾値とは、「ある行動を選択するために、他者が何人（あるいは何割）その行動をとっている必要があるか」を示す数値である ¹。

ある個人 $i$ が行動（例えば、拍手をする、商品を購買する、暴動に参加する）を選択する場合の効用関数 $U_i$ は以下のように定式化できる。

$U_i(n) = B_i(n) - C_i(n)$

ここで、 $n$ は既に行動している他者の数、 $B_i$ は行動による利益、 $C_i$ はコストである。

プレゼンテーションの文脈では、コスト $C$ は「目立つことによる社会的リスク（恥、孤立）」であり、利益 $B$ は「集団への帰属感」や「承認欲求の充足」となる。

誰も行動していない時（ $n=0$ ）、コストは最大となる。しかし、他者が行動するにつれて（ $n$ が増加）、コストは減少し、逆に「自分だけ参加していない」という新たなコスト（同調圧力）が発生するため、参加のベネフィットが相対的に高まる。

閾値はこの損益分岐点である。

閾値0（イノベーター／扇動者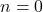）: $n=0$ でも行動する。彼らは内部動機が強く、社会的コストを無視できる ⁶。
閾値1（初期フォロワー）: 1人が行動すれば、自分も参加する。
閾値50（マジョリティ）: 半数の人が行動して初めて重い腰を上げる。
閾値100（頑固者）: 全員が行動しても参加しない ⁷。

1.3 暴動のモデル：連鎖反応の微細構造

グラノヴェッターが示した最も衝撃的なシミュレーションは、閾値の分布がわずかに異なるだけで、結果が天と地ほど変わるという事例である ⁴。

ここに100人の群衆がいると仮定する。彼らは潜在的にある行動（例えばスタンディングオベーション）を起こす可能性がある。

シナリオA：完全な連鎖（革命の成功）

群衆の閾値分布は以下の通りである。

閾値0：1人
閾値1：1人
閾値2：1人
…
閾値99：1人

この場合、何が起きるか。

まず、閾値0の人物が立ち上がる。
閾値1の人物は、1人が立っているのを見て、「閾値を超えた」と判断し立ち上がる。
現在立っているのは2人である。閾値2の人物は、2人が立っているのを見て立ち上がる。
このドミノ倒しは最後まで続き、最終的に100人全員が立ち上がる。

シナリオB：途切れた連鎖（沈黙の支配）

群衆の分布がわずかに異なるとする。

閾値0：1人
閾値1：0人
閾値2：2人
閾値3：1人
…

この変更は微細である。平均的な選好度はシナリオAとほぼ変わらない。しかし、結果は劇的に異なる。

閾値0の人物が立ち上がる。
次に立ち上がるべき候補者は「閾値1」の人物だが、この集団には存在しない。
その次に意欲が高いのは「閾値2」の人物たちである。しかし、彼らが立ち上がる条件は「2人が行動していること」である。現在立っているのは閾値0の1人だけである。
したがって、閾値2の人物は動かない。
連鎖はここで停止する。結果、100人のうち行動したのはたった1人である。

この数理モデルが示唆する事実は重い。プレゼンテーションにおいて「聴衆の反応が悪い」と感じる時、それは必ずしもコンテンツがつまらないからではない。また、聴衆の平均的な関心が低いからでもない。単に、反応の連鎖をつなぐ**「閾値1」や「閾値2」の人物が、物理的に欠落していたか、あるいは機能しなかった**だけである可能性が高い ⁴。

1.4 平衡状態の分析：静止相と流動相

このモデルにおける「平衡状態（Equilibrium）」とは、もはや誰も行動を変えなくなった時点を指す 1。

シナリオAの平衡状態は「全員参加（流動相・活性相）」であり、シナリオBの平衡状態は「1名のみ参加（静止相・凍結相）」である。

プレゼンターの役割は、会場を「不安定な平衡状態」に置くことである。つまり、ほんの少しの刺激（閾値0の発火）で、システム全体が別の平衡状態へと雪崩を打つような「クリティカル（臨界）」な状態を準備することにある。逆に、どんなに素晴らしいスピーチをしても、会場の構造がシナリオBのように断絶していれば、そのエネルギーは熱として散逸し、集団行動という仕事には変換されない。

第2章社会物理学とイジングモデル

グラノヴェッターのモデルは社会学的なアプローチであるが、物理学の視点から見ると、これは強磁性体の相転移を記述する「イジングモデル（Ising Model）」と等価な構造を持っていることがわかる ⁹。このアナロジーを用いることで、プレゼンテーションの力学をより精緻に、変数を操作可能な形で理解することができる。

2.1 磁性体としての聴衆

イジングモデルでは、物質を構成する原子が「スピン」と呼ばれる磁気モーメントを持つと考える。スピンは上向き（+1）か下向き（-1）のいずれかの状態をとる。

スピン上向き（+1）：提案に賛成、拍手する、笑う
スピン下向き（-1）：提案に反対、腕を組む、無表情

通常の状態（高温状態）では、スピンはバラバラの方向を向いており、全体としての磁力（集団の意思）はゼロである。しかし、ある条件を満たすと、全てのスピンが一斉に同じ方向を向き、強力な磁石となる。これがプレゼンテーションにおける「会場の一体化」である。

2.2 スピン、相互作用、外部磁場

個々の聴衆（スピン $S_i$ ）の状態を決定するエネルギー関数（ハミルトニアン）は、物理学では以下のように表される。

$E = -J \sum S_i S_j - H \sum S_i$

この式は、プレゼンテーションの成否を握る2つの主要な力を記述している。

相互作用項 ( $J \sum S_i S_j$ ):
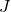- $J$ は「交換相互作用」の強さを表す。社会物理学的には、これは「隣人の影響力」や「同調圧力の強さ」に相当する ⁹。
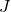- $J$ が正の値で大きければ大きいほど、隣り合う人は同じ行動（同じスピンの向き）を取りたがる。
- グラノヴェッターのモデルにおける「他者の行動数への依存」はこの項に対応する。
外部磁場項 ( $H \sum S_i$ ):
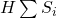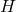- $H$ は外部から加えられる磁場である。これは「プレゼンターの影響力」や「コンテンツの説得力」に相当する ¹⁰。
- 多くのプレゼンターは、この 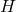$H$ （自分の話し方、スライドの質）を高めることに注力する。

しかし、イジングモデルが教える重要な教訓は、相転移（劇的な変化）を引き起こす主役は $H$ （プレゼンター）ではなく、 $J$ （聴衆同士の相互作用）であるという点だ。外部磁場 $H$ が弱くても、相互作用 $J$ が十分に強ければ、自発的磁化（自発的なスタンディングオベーション）は発生する。逆に、 $J$ がゼロ（聴衆同士がお互いを無視している状態）であれば、どれだけ強力な $H$ を加えても、個々人をバラバラに説得するしかなく、爆発的な感染は起きない。

2.3 温度（社会的ノイズ）の役割

物理モデルには「温度 $T$ 」という変数が存在する。温度が高いと、熱ゆらぎによってスピンはランダムに動こうとする。

社会物理学において、この「温度」は「社会的ノイズ」や「曖昧さ」、あるいは「個人の気まぐれ」と解釈できる 9。

低温状態: 聴衆は理性的かつ機械的に、周囲やプレゼンターの影響に反応する。決定論的である。
高温状態: 聴衆は注意散漫であったり、酔っていたり、あるいは個々人の事情（トイレに行きたい、機嫌が悪い）によってランダムな行動をとる。

一見すると、ノイズ（温度）は邪魔なものに思える。しかし、グラノヴェッター・モデルのシミュレーション研究において、「確率共鳴」に似た興味深い現象が確認されている。完全に決定論的な集団（温度ゼロ）よりも、適度なノイズ（ゆらぎ）を持つ集団の方が、情報の伝播や行動の連鎖がスムーズに行われる場合があるのだ 13。

これは「予測可能性のパラドックス」と呼ばれる。第1章の「シナリオB」のように、閾値1の人が欠けて連鎖が止まってしまうような硬直的な状況でも、適度なノイズ（閾値2の人が気まぐれで動くなど）があれば、そのギャップを飛び越えて連鎖が再開する可能性があるからだ 13。

2.4 相転移のメカニズム

プレゼンテーションの進行は、聴衆という系の温度を下げつつ（集中させ）、相互作用 $J$ を高め（一体感を作り）、臨界点を超えさせるプロセスであると言える。

物理学において、相転移点近傍では「臨界減速」や「ゆらぎの増大」といった特徴的な現象が見られる。社会集団においても、大きな変化が起きる直前には、局所的な小集団でのざわめきや、同調行動の予兆（小さな頷きの波）が観測される。これを敏感に察知し、そこにエネルギーを注入できるかが、熟練プレゼンターと初心者の分水嶺となる。

第3章ネットワーク構造と影響力の重み付け

グラノヴェッターの初期モデルは、全員が全員を見渡せる「完全結合ネットワーク」を仮定していた。しかし、現実の会場や社会ネットワークには構造がある。誰が誰の隣に座っているか、誰が誰の友人であるかによって、影響力の伝わり方は不均一になる。

3.1 強い紐帯と弱い紐帯のパラドックス

グラノヴェッターの名声を不動のものにしたのは1973年の論文「弱い紐帯の強み（The Strength of Weak Ties）」である ¹⁴。彼は、家族や親友といった「強い紐帯（Strong Ties）」よりも、知人や同僚といった「弱い紐帯（Weak Ties）」の方が、新規情報の伝播には重要であると説いた。強い紐帯は閉じたクラスター（集団）を形成しやすく、情報がその中で循環してしまうからである。

しかし、行動の変容（プレゼンで説得され、行動を起こすこと）においては、話が逆転する。情報の伝達には「弱い紐帯」が有効だが、リスクを伴う行動の採用には「強い紐帯」からの確証が必要となる ¹⁶。これを「複雑な伝染（Complex Contagion）」と呼ぶ。

3.2 友人対他者：影響力の倍率（2xルール）

プレゼンテーションの会場において、隣に座っているのが「友人」か「見知らぬ人」かは、閾値計算に決定的な重み付けを与える。

複数の研究やグラノヴェッター自身の示唆によれば、社会的影響力において、友人の行動は他人の行動の約2倍の重みを持つとモデル化できる 18。

数式で表せば、ある個人 $i$ が感じる社会的圧力 $P_i$ は以下のように修正される。

$P_i = \sum_{j \in \text{Friends}} 2 \cdot S_j + \sum_{k \in \text{Strangers}} 1 \cdot S_k$

これは、閾値20の人間を動かすために、見知らぬ人なら20人の行動が必要だが、友人なら10人で済むことを意味する。

この「2xルール」は、会場の座席配置や、「サクラ」の配置戦略に直結する。見知らぬ人の中にポツンとサクラを配置するよりも、互いに友人関係にある集団をまるごと動かす方が、局所的な圧力ははるかに高くなる。

3.3 クラスター係数と情報の伝播

最近のネットワーク科学の研究（Zhang et al., 2015など）では、ネットワークが小さい場合（小規模なセミナーなど）は友人の行動観察が有効だが、ネットワークが巨大化するにつれて、見知らぬ他者の総数（「みんながやっている」という事実）の影響力が増大することが示されている ¹⁶。

しかし、クリティカル・マス（臨界量）に達するまでの初期段階では、友人の影響が支配的である。したがって、プレゼンテーションの初期段階では、会場内に存在する既存の人間関係（同僚同士のグループ、上司と部下）のラインに沿って同意を形成していくことが、最も効率的な相転移のルートとなる。

逆に、全く人間関係のないバラバラの聴衆（公開セミナーなど）の場合、影響力の重み係数が低いため、相転移を起こすために必要なエネルギー（プレゼンターの熱量 $H$ ）は、より高いものが要求されることになる。

第4章クリティカル・マスとティッピング・ポイント

では、具体的にどれだけの人数を動かせば、集団全体の相転移は不可避となるのか。グラノヴェッターのモデルは分布の重要性を説いたが、その後の実験社会科学は、より具体的な「転換点」の数値を導き出している。

4.1 25%の法則：社会変革の閾値

ペンシルベニア大学のDamon Centolaらによる最近の研究（2018年、Science誌）は、社会的な規範が変わるためのティッピング・ポイント（転換点）が、集団の約25%にあることを実験的に証明した ²¹。

この実験では、集団内にある規範を定着させた後、少数の「改革派（サクラ）」を投入して逆の規範を広めようと試みた。改革派の比率が10%未満のときは、彼らの行動は単なるノイズや逸脱として処理され、マジョリティに吸収されてしまった。しかし、改革派の比率が25%を超えた瞬間、集団全体の動向が劇的に反転し、残りの75%が一気に新しい規範（行動）へと雪崩れ込んだのである ²³。

この「25%ルール」は、プレゼンテーション戦略における「マジックナンバー」となる。

聴衆全員を説得する必要はない。また、過半数（51%）を確保する必要さえない。「会場の25%」という確固たる橋頭堡（きょうとうほ）を築くことができれば、あとは社会物理学の法則が残りの75%を飲み込んでくれるのである。

4.2 少数派が多数派を覆すメカニズム

なぜ25%なのか。これには「調整ゲーム（Coordination Game）」の理論が関わっている。

人々は「正しいこと」をしたいという欲求と同時に、「多数派側にいたい（勝ち馬に乗りたい）」という強力な欲求を持っている。

参加者が25%を超えると、それはもはや「変わり者の集団」ではなく、「無視できない対抗勢力」として認識される。残りの多数派にとって、「現状維持」を続けることの社会的コスト（もし新しい波が勝ったら、自分は取り残されるというリスク）が急上昇する 25。

プレゼンテーションにおいて、肯定的な反応（頷き、笑い、メモを取る）を示す層が25%を超えると、残りの層は「自分が理解できていない重要なことが話されているのではないか」という不安（FOMO: Fear Of Missing Out）に駆られ始める。これが、中立層を一気に肯定層へと転向させる駆動力となる。

4.3 プレゼンテーションにおける「サクラ」の科学

グラノヴェッターの理論と25%ルールを組み合わせると、「サクラ（Plants）」あるいは「協力者」の科学的な運用法が見えてくる。

倫理的な是非はさておき、純粋に力学的な観点からは、サクラの役割は「拍手の音量を上げること」ではない。彼らの役割は「閾値の連鎖の断絶を防ぐこと」にある。

配置戦略: サクラを分散させてはいけない。第3章で見たように、彼らを固めて配置し、局所的な「過半数」を作り出すべきである。イジングモデルにおいて、局所的に揃ったスピンの塊（磁区）が成長して全体を覆うように、サクラの塊が周囲の閾値の低い層を巻き込みながら拡大していく ⁹。
タイミング: 彼らは「閾値0」として振る舞うべきである。しかし、より重要なのは、一般の聴衆の中から「閾値1」の人物が現れた瞬間に、それを全力で肯定し、サポートする「閾値2」としての役割である。これにより、自発的な反応の火種を消さずに、連鎖反応へと導くことができる。

第5章場の空気（Kuuki）の研究

日本社会において、集団行動を論じる上で避けて通れないのが「空気」の概念である。山本七平が「空気の研究」で論じたように、日本では論理的妥当性よりも「その場の空気」が決定権を持つことが多い。グラノヴェッター・モデルの視点から、この「空気」を物理量として再定義する。

5.1 日本的文脈における「空気」の物理量

社会物理学的に定義するならば、「空気（Kuuki）」とは、「集団の秩序変数（Order Parameter）の可視化された状態」である ²⁶。

KY（空気読めない）: これは、局所的な相互作用 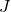$J$ によって形成された秩序変数（スピンの向き）に逆行する行動をとる個人のことである ²⁸。

グラノヴェッターのモデルにおいて、閾値とは「他者の行動数への依存度」であった。日本社会における「空気を読む」という行為は、個々人が極めて高い相互作用係数 $J$ を持っている状態、あるいは全員が高い閾値（自分からは動かないが、周りが動けば動く）を持っている状態として記述できる。

これは系全体が「超過敏」な状態にあることを意味する。誰も動かない静寂（静止相）は強固に見えるが、ひとたび誰かが動いてそれが「新しい空気」として認知されると、全員が一斉にそちらへ動く（雪崩現象）。日本の組織や聴衆が見せる「全会一致」や「満場一致」の背後には、このような高相互作用・高閾値の力学が働いている。

5.2 多多元的無知（Pluralistic Ignorance）の打破

「空気」の正体の一つに、「多元的無知（Pluralistic Ignorance）」がある 4。

これは、「個々人の内面では反対している（あるいは賛成している）にもかかわらず、他者もそう思っているだろうと誤認し、集団としては本心と逆の行動をとる」現象である。

プレゼンの質疑応答で誰も手を挙げない時、多くの聴衆は「質問がない」のではなく、「質問するのは自分だけかもしれない（恥ずかしい）」と思っている。全員がそう思っているため、結果として沈黙が続く。

この「偽りの平衡状態」を破るには、プレゼンターが「隠れた閾値の可視化」を行う必要がある。

「隣の方と今の感想を話してください」という指示は、隣人の本心（スピンの状態）を確認させ、多元的無知を解消する強力な手法である。隣人が「今の話、面白かったね」と言えば、その瞬間に「賛同すること」の社会的コストはゼロになり、閾値の連鎖が一気に進む。

5.3 同調圧力の力学

同調圧力（Peer Pressure）は、物理学的には「スピンを揃えようとするエネルギー」である。

プレゼンターにとって、同調圧力は敵にも味方にもなる。

敵: 初期段階。聴衆は「無反応」という同調圧力の中にいる。
味方: 相転移後。一度「反応する」という空気ができれば、同調圧力は残りの懐疑的な層を強制的に拍手させる力として働く。

重要なのは、同調圧力のベクトルをいつ反転させるかである。そのトリガーとなるのが、前述の「25%のクリティカル・マス」の達成である。25%を超えた瞬間、同調圧力のベクトルは「静寂」から「熱狂」へと反転する。

第6章拍手の物理学：蔵本モデルと同期現象

プレゼンテーションのクライマックスである「拍手」や「スタンディングオベーション」は、単なる行動の総和ではなく、リズムの同期現象を含んでいる。ここでは、同期現象の数理モデルである「蔵本モデル（Kuramoto Model）」を導入する。

6.1 非同期から同期への転移

拍手には2つのフェーズがあることが物理学的研究で知られている ²⁹。

非同期フェーズ（Incoherent Phase）: 聴衆が個別のタイミングで手を叩く。パラパラという雷雨のような音。
同期フェーズ（Synchronized Phase）: 全員の拍手の周期が揃い、リズミカルな手拍子になる。

蔵本モデルによれば、個々の振動子（聴衆）の結合強度 $K$ （他者の音を聞いて合わせようとする意識）がある臨界値 $K_c$ を超えると、自然に同期が発生する 30。

興味深いことに、拍手が同期してリズミカルになると、全体の音量は下がる傾向がある（全員が同時に叩くため、隙間ができる）。しかし、聴衆は「一体感」を強く感じる。そして、その一体感を維持しようとするあまり、拍手をやめるタイミングを逸し、拍手が不自然に長く続く現象が起きる 31。

6.2 空間的伝播と視覚的結合

拍手の開始と伝播は、感染症モデル（SIRモデル）や森林火災モデルに近い挙動を示す 31。

拍手はランダムに発生するのではなく、発生源（イノベーター）から空間的に、隣接する席へと波紋のように広がる。

ここで重要なのが「視覚的結合」である。音（聴覚）だけでなく、他者が叩いている姿（視覚）は、結合強度 $K$ を劇的に高める。

実践的洞察:

スタンディングオベーションを引き起こしたい場合、プレゼンターは「会場を明るくする」べきである。

暗い会場では、視覚的な情報（他者が立っている姿）が遮断され、結合強度が下がるため、同期（相転移）が起きにくい。明るい会場で互いの姿を確認できる環境こそが、グラノヴェッターの連鎖と蔵本モデルの同期を促進する物理的条件である。

第7章プレゼンテーション・エンジニアリング（実践編）

ここまでの理論的背景（閾値モデル、ネットワーク理論、イジングモデル、クリティカル・マス）を統合し、プレゼンターが実行可能な具体的なエンジニアリング手法を提示する。

7.1 会場設計と座席のトポロジー

プレゼンテーションの成否は、スライドを作る前、会場のレイアウトを決める段階で半分決まっている。

密度を高める: イジングモデルにおいて、スピン間の距離が近いほど相互作用 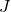$J$ は強まる。空席が目立つスカスカの会場では、影響力の連鎖が物理的に途切れる。定員100人の部屋に50人を入れるより、定員50人の部屋に50人を詰め込む方が、相転移は起きやすい。
強い紐帯のクラスタリング: 知り合い同士、同僚同士を固めて座らせる。これにより、局所的な影響力の倍率（2xルール）を最大化し、発火しやすい「ホットスポット」を作る。
前方の確保: 閾値の低い肯定的な聴衆（ファン、関係者）を前方に配置する。彼らの反応は背後の聴衆の視界に入るため、視覚的な連鎖反応の起点となる。逆は最悪である。前方に不機嫌な「閾値100」の人物が座ると、それは防波堤となり、後ろへの連鎖を遮断する。

7.2 初期着火（イグニッション）の技術

プレゼン開始直後の数分間は、系の「温度」と「初期磁化」を決定する重要なフェーズである。

閾値0の発見と承認: 頷いている人、笑顔の人を素早く見つける。彼らと視線を合わせ、語りかけることで、彼らの行動（頷き）を強化する。
閾値1の代行: もし「最初の質問者」が出ない場合、あるいは「最初の笑い」が起きない場合、プレゼンター自身がその役割を演じるか、ハードルを下げる。「よく、こんな質問をされますが…」と自ら口火を切ることで、閾値1の不在というギャップを埋める ³²。
デレク・シヴァーズの教え: 「最初のフォロワー」が出た瞬間、プレゼンターは彼らを過剰なほどに称賛し、受け入れなければならない。それはその個人への礼儀ではなく、後に続く閾値2～99の人々に対する「安全性」のシグナリングである ³³。

7.3 質疑応答の連鎖設計

質疑応答セッションは、最も閾値モデルが顕著に現れる場である。

サクラ質問の効用: 最初の1人が手を挙げるかどうかが、その後の全ての流れを決める。最初の質問者をあらかじめ仕込んでおく（閾値0を用意する）ことは、不正というよりは、会場のポテンシャルエネルギー障壁を超えるための「触媒」として機能する。
挙手の可視化: 「質問がある人は？」と聞くのではなく、「これについて同じように悩んだことがある人は手を挙げてください」と、低コストの行動（投票）を挟む。これにより、会場内に潜在する「仲間」の存在が可視化され、個人の閾値が下がる。

結論

本報告書は、プレゼンテーションを「情報の伝達」ではなく「集団の相転移現象」として再定義した。マーク・グラノヴェッターの閾値モデルは、なぜ優れたコンテンツが無視され、平凡な扇動が熱狂を生むのかという謎に対し、冷徹な数理的解答を与える。

それは「連鎖の連続性」の問題である。

どんなに熱量の高い火種（プレゼンター）があっても、薪（聴衆）の並び方に隙間があれば火は燃え移らない。逆に、適切な位置に「導火線」となる人々（閾値0, 1, 2…）が配置され、相互作用のネットワークが密に設計されていれば、わずかな火花で会場全体を燃え上がらせることができる。

社会物理学の知見が示唆するのは、プレゼンターは「演者」であると同時に「物理学者」でなければならないということだ。会場の温度を感じ、結合強度を高め、クリティカル・マス（25%）を見極め、意図的に相転移のスイッチを押す。

戦略1: 聴衆の平均ではなく、分布（特に低閾値層の連続性）に注目せよ。
戦略2: 友人関係と物理的距離を利用して、相互作用 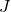$J$ を最大化せよ。
戦略3: 25%の熱狂を作り出し、同調圧力のベクトルを反転させよ。
戦略4: 空気を読むのではなく、空気を構成するパラメータ（視認性、音、密度）を操作せよ。

この科学的アプローチを採用することで、プレゼンテーションは不確実な「賭け」から、再現性のある「エンジニアリング」へと昇華されるのである。

表1：社会システムと物理システムの対応表

社会システム（プレゼンテーション）	物理システム（イジングモデル／相転移）	意味・役割
個々の聴衆	原子（スピン）	システムの最小構成要素
行動（拍手／沈黙）	スピンの向き（+1 / -1）	観測される状態
隣人との関係性・同調	交換相互作用 ( $J$ )	隣と同じ状態になろうとする力
プレゼンターの説得力	外部磁場 ( $H$ )	全体の向きを強制的に変えようとする力
会場の集中力・ノイズ	温度 ( $T$ )	ランダムな動きを引き起こすゆらぎ
熱狂・スタンディングオベーション	強磁性相（自発磁化）	全体の秩序が整った状態
場の空気 (Kuuki)	秩序変数	システム全体のマクロな状態量
サクラ・熱狂的ファン	不純物・核形成サイト	相転移のきっかけとなる欠陥
クリティカル・マス (25%)	臨界点 ( $T_c$ )	状態が急激に変化する閾値

本分析が、読者の皆様の次なるプレゼンテーションにおける「相転移」の設計図となることを願う。

引用文献

[PDF] Threshold Models of Collective Behavior | Semantic Scholar, https://www.semanticscholar.org/paper/Threshold-Models-of-Collective-Behavior-Granovetter/92b6aeb4e4f8e0c170f33ba274ce1830db9c9496
Threshold Models of Collective Behavior | American Journal of Sociology: Vol 83, No 6, https://www.journals.uchicago.edu/doi/abs/10.1086/226707
Threshold Models of Collective Behavior – Stanford Sociology, https://sociology.stanford.edu/publications/threshold-models-collective-behavior
Threshold Models of Collective Behavior II: The Predictability Paradox and Spontaneous Instigation – Sociological Science, https://sociologicalscience.com/download/vol-7/december/SocSci_v7_628to648.pdf
Threshold Models of Collective Behavior – SIU Computer Science, https://www.cs.siu.edu/~hexmoor/classes/CS539-F10/Collective-Behavior.pdf
Do you wanna riot? Thinking about group behaviour from the perspective of individual preferences | Social in silico, https://socialinsilico.wordpress.com/2014/01/15/do-you-wanna-riot-thinking-about-group-behaviour-from-the-perspective-of-individual-preferences/
Granovetter’s threshold model – Physics of Risk, https://rf.mokslasplius.lt/granovetters-threshold-model/
threshold models of collective behavior mark granovetter, https://www.pushkin.fm/wp-content/uploads/imported-files/granovetter78threshold.pdf
(PDF) Sociophysics models inspired by the Ising model – ResearchGate, https://www.researchgate.net/publication/396025910_Sociophysics_models_inspired_by_the_Ising_model
[2506.23837] Sociophysics models inspired by the Ising model – arXiv, https://arxiv.org/abs/2506.23837
Full article: Interpreting the Ising Model: The Input Matters, https://www.tandfonline.com/doi/full/10.1080/00273171.2020.1730150
Dynamical phase transitions in Markov processes by Hugo Touchette – YouTube, https://www.youtube.com/watch?v=_rBzf3JqBpc
(PDF) Threshold Models of Collective Behavior II: The Predictability Paradox and Spontaneous Instigation – ResearchGate, https://www.researchgate.net/publication/347175703_Threshold_Models_of_Collective_Behavior_II_The_Predictability_Paradox_and_Spontaneous_Instigation
The Strength of Weak Ties, https://faculty.washington.edu/matsueda/courses/590/Readings/Granovetter%20Weak%20Ties%20AJS.pdf
The Strength of Weak Ties by Mark S. Granovetter – Stanford Network Analysis Project, https://snap.stanford.edu/class/cs224w-readings/granovetter73weakties.pdf
Social Learning in Networks of Friends versus Strangers – ResearchGate, https://www.researchgate.net/publication/275247385_Social_Learning_in_Networks_of_Friends_versus_Strangers
https://ideas.repec.org/a/inm/ormksc/v34y2015i4p573-589.html#:~:text=We%20show%20that%20when%20the,network%20heterogeneity%20on%20social%20learning.
Threshold Models of Collective Behavior – SIU Computer Science, https://www2.cs.siu.edu/~hexmoor/classes/CS539-F10/Collective-Behavior.pdf
Threshold Models of Collective Behavior – Mark Granovetter, https://fbaum.unc.edu/teaching/articles/Granovetter_AJS_1978.pdf
Analysis of complex contagions in random multiplex networks | Phys. Rev. E, https://link.aps.org/doi/10.1103/PhysRevE.86.036103
Research Finds Tipping Point for Large-Scale Social Change | Annenberg, https://www.asc.upenn.edu/news-events/news/research-finds-tipping-point-large-scale-social-change
Tipping point for large-scale social change? Just 25 percent – Penn Today, https://penntoday.upenn.edu/news/damon-centola-tipping-point-large-scale-social-change
https://penntoday.upenn.edu/news/damon-centola-tipping-point-large-scale-social-change#:~:text=According%20to%20a%20new%20paper,type%20of%20movement%20or%20initiative.
The 25 Percent Tipping Point for Social Change | Psychology Today, https://www.psychologytoday.com/us/blog/how-behavior-spreads/201905/the-25-percent-tipping-point-social-change
Shaping social norms with the 25% rule – Learning Loop, https://learningloop.io/blog/25-percent-rule-social-norms
「空気を読む」- Reading the air – DiVA portal, https://www.diva-portal.org/smash/get/diva2:1861112/FULLTEXT01.pdf
Reading the Air – ArtReview, https://artreview.com/december-2015-feature-naomi-pearce-reading-the-air/
How & When to Apologize in Japan | All About Japan, https://allabout-japan.com/en/article/2833/
Applause Physics, https://physics.aps.org/story/v5/st27
(PDF) Physics of the rhythmic applause – ResearchGate, https://www.researchgate.net/publication/1821065_Physics_of_the_rhythmic_applause
The dynamics of audience applause – PMC – PubMed Central – NIH, https://pmc.ncbi.nlm.nih.gov/articles/PMC4043176/
Derek Sivers on Leadership Lessons from Dancing Guy – Ed Batista, https://edbatista.com/2010/03/dancing-guy.html
First Follower: Leadership Lessons from Dancing Guy – YouTube, https://www.youtube.com/watch?v=fW8amMCVAJQ

スティグマジーと群知能による創発的協調の設計

不確実性の数理、認知ダイナミクス、および集合的同期に関する包括的分析

プレゼンテーションの社会物理学：グラノヴェッターの閾値モデルと社会的相転移のエンジニアリング

序論：説得の科学から場の物理学へ

第1章集団行動の数理モデル：グラノヴェッターの革命

1.1 合理的選択と集団のパラドックス

1.2 閾値（Threshold）の定義と効用関数

1.3 暴動のモデル：連鎖反応の微細構造

シナリオA：完全な連鎖（革命の成功）

シナリオB：途切れた連鎖（沈黙の支配）

1.4 平衡状態の分析：静止相と流動相

第2章社会物理学とイジングモデル

2.1 磁性体としての聴衆

2.2 スピン、相互作用、外部磁場

2.3 温度（社会的ノイズ）の役割

2.4 相転移のメカニズム

第3章ネットワーク構造と影響力の重み付け

3.1 強い紐帯と弱い紐帯のパラドックス

3.2 友人対他者：影響力の倍率（2xルール）

3.3 クラスター係数と情報の伝播

第4章クリティカル・マスとティッピング・ポイント

4.1 25%の法則：社会変革の閾値

4.2 少数派が多数派を覆すメカニズム

4.3 プレゼンテーションにおける「サクラ」の科学

第5章場の空気（Kuuki）の研究

5.1 日本的文脈における「空気」の物理量

5.2 多多元的無知（Pluralistic Ignorance）の打破

5.3 同調圧力の力学

第6章拍手の物理学：蔵本モデルと同期現象

6.1 非同期から同期への転移

6.2 空間的伝播と視覚的結合

第7章プレゼンテーション・エンジニアリング（実践編）

7.1 会場設計と座席のトポロジー

7.2 初期着火（イグニッション）の技術

7.3 質疑応答の連鎖設計

結論

表1：社会システムと物理システムの対応表

引用文献

関連記事

スティグマジーと群知能による創発的協調の設計

不確実性の数理、認知ダイナミクス、および集合的同期に関する包括的分析

ハンディキャップ原理とコストのかかるシグナリング理論：AI時代における信頼の進化的・認知科学的再構築に関する包括的研究報告書

プレゼンテーションの社会物理学：グラノヴェッターの閾値モデルと社会的相転移のエンジニアリング

序論：説得の科学から場の物理学へ

第1章 集団行動の数理モデル：グラノヴェッターの革命

1.1 合理的選択と集団のパラドックス

1.2 閾値（Threshold）の定義と効用関数

1.3 暴動のモデル：連鎖反応の微細構造

シナリオA：完全な連鎖（革命の成功）

シナリオB：途切れた連鎖（沈黙の支配）

1.4 平衡状態の分析：静止相と流動相

第2章 社会物理学とイジングモデル

2.1 磁性体としての聴衆

2.2 スピン、相互作用、外部磁場

2.3 温度（社会的ノイズ）の役割

2.4 相転移のメカニズム

第3章 ネットワーク構造と影響力の重み付け

3.1 強い紐帯と弱い紐帯のパラドックス

3.2 友人対他者：影響力の倍率（2xルール）

3.3 クラスター係数と情報の伝播

第4章 クリティカル・マスとティッピング・ポイント

4.1 25%の法則：社会変革の閾値

4.2 少数派が多数派を覆すメカニズム

4.3 プレゼンテーションにおける「サクラ」の科学

第5章 場の空気（Kuuki）の研究

5.1 日本的文脈における「空気」の物理量

5.2 多多元的無知（Pluralistic Ignorance）の打破

5.3 同調圧力の力学

第6章 拍手の物理学：蔵本モデルと同期現象

6.1 非同期から同期への転移

6.2 空間的伝播と視覚的結合

第7章 プレゼンテーション・エンジニアリング（実践編）

7.1 会場設計と座席のトポロジー

7.2 初期着火（イグニッション）の技術

7.3 質疑応答の連鎖設計

結論

表1：社会システムと物理システムの対応表

引用文献

関連記事

スティグマジーと群知能による創発的協調の設計

不確実性の数理、認知ダイナミクス、および集合的同期に関する包括的分析

ハンディキャップ原理とコストのかかるシグナリング理論：AI時代における信頼の進化的・認知科学的再構築に関する包括的研究報告書

第1章集団行動の数理モデル：グラノヴェッターの革命

第2章社会物理学とイジングモデル

第3章ネットワーク構造と影響力の重み付け

第4章クリティカル・マスとティッピング・ポイント

第5章場の空気（Kuuki）の研究

第6章拍手の物理学：蔵本モデルと同期現象

第7章プレゼンテーション・エンジニアリング（実践編）